锯木厂选址

Problem

Source: 洛谷 P4360, CEOI 2004, BSOJ 2684

Description

从山顶上到山底下沿着一条直线种植了 $n$ 棵老树。当地的政府决定把他们砍下来。为了不浪费任何一棵木材，树被砍倒后要运送到锯木厂。

木材只能按照一个方向运输：朝山下运。山脚下有一个锯木厂。另外两个锯木厂将新修建在山路上。你必须决定在哪里修建两个锯木厂，使得传输的费用总和最小。假定运输每公斤木材每米需要一分钱。

你的任务是编写一个程序，读入树的个数和他们的重量与位置，计算最小运输费用。

Input

输入的第一行为一个正整数 $n$ —— 树的个数（$2 \leq n \leq 20000$）。树从山顶到山脚按照 $1, 2…n$ 标号。接下来 $n$ 行，每行有两个正整数（用空格分开）。第 $i+1$行含有：$w_i$ —— 第 $i$ 棵树的重量（公斤为单位）和 $d_i$ —— 第 $i$ 棵树和第 $i+1$ 棵树之间的距离，$1 \leq w_i \leq 10000，0 \leq d_i \leq 10000$。最后一个数 $d_n$，表示第 $n$ 棵树到山脚的锯木厂的距离。保证所有树运到山脚的锯木厂所需要的费用小于 2000000000 分。

Output

输出只有一行一个数：最小的运输费用。

Sample Input

9
1 2
2 1
3 3
1 1
3 2
1 6
2 1
1 2
1 1

Sample Output

26

Solution

状态转移方程

第 $n$ 棵树下面还有一个锯木厂，可以把它当作第 $n+1$ 个位置来考虑。

第 $1 - i$ 棵树的总重量：

第 $1 - i$ 棵树的距离：

把第一锯木场设在第 $i​$ 棵树的位置上，第 $1 - i​$ 棵树到 $i​$ 所需的费用：

把第 $i - j$ 棵木头都运送到第 $j$ 棵树的位置上所需要的费用：

$ f(i) $ 为第二个锯木厂设在 $i$ 处所需的总费用，那么状态转移方程为：

该方程的时间复杂度为 $O(n^2)$ ，而 $n \leq 20000$，因此必须对其进行优化。

斜率优化

结论 1

如果在位置 $i$ 建设第二个锯木厂，第一个锯木厂的位置是 $j$ 时最优。那么如果在位置 $i+1$ 建设第二个锯木厂，第一个锯木厂的最佳位置不会小于 $j$。

证明 1

对于 $j_1 < j_2 < i$ 来说，决策 $j_2$ 比决策 $j_1$ 优的条件是：

化简：

又因为 $Sw(i)$ 单调递增，$j_1 < j_2$，所以 $Sw(j_1) - Sw(j_2)<0​$，则：

令 $\text{Slope}(j_1, j_2) =$ 不等式左边，表示斜率。

根据 $(1)​$ 式推导出来的式子有：

1. $\text{Slope}(j_1, j_2) < Sd(i)$：决策 $j_2$ 比决策 $j_1$ 优

2. $\text{Slope}(j_1, j_2) \geq Sd(i)$：决策 $j_1$ 比决策 $j_2$ 优

因为 $Sd(i)>0$ 且随着 $i$ 的增大而增大，所以对于 $k \geq i$ 时，$Sd(k) \geq Sd(i)$，故 $\text{Slope}(j_1, j_2) < Sd(i) \leq Sd(k)$。即如果对于 $i$ 来说 $j_2$ 比 $j_1$ 优，那么对于 $k$ 来说至少也是 $j_2$ 比 $j_1$ 优。

单调队列维护

上面的证明可以说明决策变量 $j$ 是单调的，因此可以维护一个单调队列 $q$，这个队列只能从队尾插入，但是可以从两端删除。

这个队列满足以下性质：

1. $j_1 < j_2 < j_3 < \dots < j_n$
2. $\text{Slope}(j_1, j_2) < \text{Slope}(j_2, j_3) < \dots$

意味着在同等情况下，$j_2$ 比 $j_1$ 优，$j_3$ 比 $j_2$ 优，以此类推。但 $ \text{Slope}(j_1, j2)$ 还和当前的 $Sd(i)$ 有关系，而 $Sd(i)$ 也是递增的，所以当 $\text{Slope}(j_1, j_2) < Sd(i)$ 时，$\text{Slope}(j_1, j_2)$ 对于以后的状态就没有意义，$j_1$ 就要出队。

每个 $k$ 都是进队出队 1 次，并且此队列的队头肯定是状态转移的最优值。对于 $j$ 来说，必须要构造一个 $j_1$ 与 $j_2$ 之间的关系，这个关系必须保证 $j_1<j_2$。也就是 $j$ 在单调递增时，那个关系也必须单调（像本题中的 $\text{Slope}$ 的关系），并且 $j$ 与当前的状态 $i$ 没有直接的关系。

下图用图形更形象地展现上面两个性质：

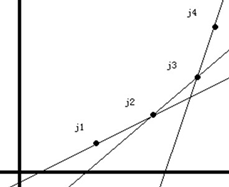
队列所需要满足的就是一个下凸的性质。根据以上的两个性质，对队列的维护进行以下 2 个操作：

设该队列为 $List$，其中 $h$ 为队头坐标，$t$ 为队尾坐标。

1. 在计算 $f(i)$ 之前，从队头开始扫描，若当前 $\text{Slope}(q(h), q(h+1))< Sd(i)$，也就是说 $q(h+1)$ 比 $q(h)$ 更优，则删除队头 $q(h)$ 元素；

2. 在计算 $f(i)$ 之后，将 $i$ 添加到队尾，并维护好队列的性质 2​。

我们面临以下两种情况：

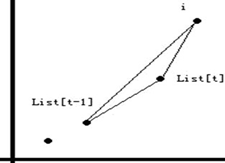
1. $\text{Slope}(q(t-1), q(t)) < \text{Slope}(q(t), i)​$

   这显然满足性质 2，于是把 $i$ 加入队列，如图：

   

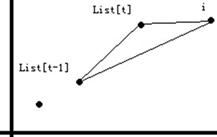
2. $\text{Slope}(q(t-1), q(t)) \geq \text{Slope}(q(t), i)$，如图：

   

结论 2

当 $a < b < c < i​$ 时，如果有 $\text{Slope}(a, b) > \text{Slope}(b, c)​$，那么 $b​$ 永远都不会成为计算 $f(i)​$ 的决策点。

证明 2

如果 $\text{Slope}(a, b) > \text{Slope}(b, c)$，那么可以分两个方面考虑 $\text{Slope}(a, b)$ 与 $Sd(i)​$ 的关系：

1. 如果 $\text{Slope}(a, b) \geq Sd(i)$，那么决策 $a$ 优于决策 $b$，即决策 $b$ 不可能是决策点；

2. 如果 $\text{Slope}(a, b) < Sd(i)$，由于 $\text{Slope}(a, b)>\text{Slope}(b, c)$，所以 $\text{Slope}(b, c)<Sd(i)$，那么决策 $c$ 要比决策 $b$ 好，所以 $b$ 还是不能作为决策点。

所以有了 $i$ 决策后，就没必要有 $q(t)$ 了，于是删除 $q(t)$。

时间复杂度

每个状态 $f(i)$ 计算的复杂度都为 $O(1)$，维护队列 $k$ 的总复杂度为 $O(n)$，因此整个算法的时间复杂度为 $O(n)$。

Code

Github (C++)

#include <iostream>
#include <cstdio>
#include <iomanip>
#include <cstring>
#include <algorithm>
#include <cmath>
using namespace std;

const int M = 20005;
int f[M], Sw[M], Sd[M], Cost[M], q[M], w[M], d[M];
//Cost[i]: 把第一锯木场设在第i棵树的位置上, 1~i 棵树到 i 所需的费用
//Sw[i]: 1~i 棵树的总重量, Sd[i]: 1~i 棵树的距离
//F[i]: 第二个锯木厂设在 i 处所需的总费用
int n, Ans = 1 << 30;

double Slope(int x, int y) {
    return (double(Sw[x] * Sd[x] - Sw[y] * Sd[y]) / double(Sw[x] - Sw[y]));
}

void Init() {
    scanf("%d", &n);
    for(int i = 1; i <= n; i++) {
        scanf("%d%d", &w[i], &d[i]);
        Sd[i] = Sd[i-1] + d[i-1];
        Sw[i] = Sw[i-1] + w[i];
    }
    Sd[n+1] = Sd[n] + d[n], Sw[n+1] = Sw[n];
    for(int i = 1; i <= n+1; i++) Cost[i] = Cost[i-1] + Sw[i-1] * d[i-1];
}

void Dp() {
  int L = 1, R = 1, j;

    for(int i = 1; i <= n; i++) {
        while(Slope(q[L], q[L+1]) < Sd[i] && L < R) L++;
        j = q[L];
        f[i] = Cost[n+1] - Sw[j] * (Sd[i] - Sd[j]) - Sw[i] * (Sd[n+1] - Sd[i]);
        /*
        W[i,j]: 把第 i~j 棵木头都运送到第 j 棵树的位置上所需要的费用
        W[i][j] = Cost[j] - Cost[i-1] - Sw[i-1] * (Sd[j] - Sd[i-1])

        f[i] = Cost[j] + W[j+1][i] + W[i+1][n+1]
            = Cost[j] + Cost[i] - Cost[j] - Sw[j] * (Sd[i] - Sd[j]) - Cost[n+1] - Cost[i] - Sw[i] * (Sd[n+1] - Sd[i])
            = Cost[n+1] - Sw[j] * (Sd[i] - Sd[j]) - Sw[i] * (Sd[n+1] - Sd[i])
        */
        while(Slope(q[R-1], q[R]) > Slope(q[R], i) && R > L) R--;
        q[++R] = i;
        Ans = min(Ans, f[i]);
    }
    printf("%d\n", Ans);
}

int main() {
    Init();
    Dp();
    return 0;
}