土地购买

Problem

Source: BZOJ 1597, USACO 2008 March Gold

Description

农夫John准备扩大他的农场，他正在考虑 $N(1 \leq N \leq 50,000)$ 块长方形的土地。每块土地的长宽满足：$1 \leq$ 宽 $\leq 1,000,000$；$1 \leq$ 长 $\leq 1,000,000$)。

每块土地的价格是它的面积，但 FJ 可以同时购买多快土地。这些土地的价格是它们最大的长乘以它们最大的宽，但是土地的长宽不能交换。如果 FJ 买一块 $3 \times 5$ 的地和一块 $5 \times 3$ 的地，则他需要付 $5 \times 5=25$。

FJ 希望买下所有的土地，但是他发现分组来买这些土地可以节省经费。他需要你帮助他找到最小的经费。

Input

第 $1$ 行：一个数 $N$；
第 $2 \dots N+1$ 行：第 $i+1$ 行包含两个数，分别为第 $i$ 块土地的长和宽。

Output

第一行：最小的可行费用。

Sample Input

Sample Output

Output Details

FJ 分 3 组买这些土地：第一组 $100 \times 1$，第二组 $1 \times 100$，第三组 $20 \times 5$ 和 $15 \times 15$。每组的价格分别为 $100,100,300$，总共 500。

Solution

Solution 1: 单调队列

将所有土地按照长度降序排列，依次检索，则当前土地的长度必然在上一块土地之内，所以只需要考虑宽度。而在宽度的问题上，当前土地的行为只能是：和前面若干块土地绑定，同时这些绑定的土地和他们前后的土地分离。这样很容易得出状态转移方程：

\[f(i) = \min_{j=0}^{i-1} \left \{ f(j) + \left ( \max_{k=j+1}^{i} w[k] \right ) * l[j+1] \right \}\]

这个方程还不能满足决策单调性，需要再做一下简化。如果将每一个土地的尺寸看成是一个二维坐标：

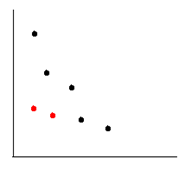
不难看出，红色点完全可以忽略。故应先将所有的土地按 $x$ 升序排列，$x$ 相同的按照 $y$ 从小到大排序。然后对于任意一个 $(x_i,y_i)$，如果存在 $(x_j, y_j)$ 满足 $x_i \leq x_j$ 且 $y_i \leq y_j$，那么 $(x_i,y_i)$ 是完全没有意义的，可以删去；所以此时得到的所有土地满足 $x$ 升序排列，$y$ 降序排列，即 $x_1 < x_2 < \dots < x_n$；$y_1 > y_2> \dots > y_n$。

然后着重看不能被忽略的这些点，它们的排布方式必然是 $x$ 单调递增，$y$ 单调递减。因此状态转移方程为：

\[f(i) = \min_{j=0}^{i-1} \Big \{ f(j) + x[i]*y[j+1] \Big \}\]

这个转移方程就是标准的决策单调性，可以通过 $w$ 函数的性质直接证明它。时间复杂度 $O(n \log n)$。

Code 1

Github (C++)

#include <iostream>
#include <cstdio>
#include <iomanip>
#include <cstring>
#include <algorithm>
#include <cmath>
using namespace std;

typedef long long ll;

const int M = 50005;

struct WE_ARE {
    int St, Ed, Sta;
} q[M];

struct THE_WORLD {
    ll a, b;
} L[M], Land[M];

ll n, N, f[M];

bool cmp(THE_WORLD x, THE_WORLD y) {
    return x.a < y.a;
}

ll Cal(int i, int j) {
    return f[j] + Land[i].b * Land[j+1].a;
}

int BiSearch(int l, int r, int t, int x) {
    int L = l, R = r, Mid;
    while(L < R) {
        Mid = (L + R) >> 1;
        if (Cal(Mid,t) >= Cal(Mid,x)) R = Mid;
        else L = Mid + 1;
    }
    if(L == r && Cal(L,x) > Cal(L,t)) return L + 1;
    return L;
}

void Dp() {
    int L = 1, R = 1;
    q[1].Sta = 0, q[1].St = 1, q[1].Ed = n;

    for(int i = 1; i <= n; i++) {
        while (L < R && q[L].Ed < i) L++;
        f[i] = Cal(i, q[L].Sta);
        while (L <= R && Cal(q[R].St, i) <= Cal(q[R].St, q[R].Sta)) R--;

        if(L <= R) {
            int w = BiSearch(q[R].St, q[R].Ed, q[R].Sta, i);
            if(w <= n) {
                if(w > q[R].St) {
                    q[R].Ed = w - 1;
                    q[++R].St = w;
                    q[R].Ed = n;
                }
                q[R].Sta = i;
            }
        }
        else q[++R].St = i + 1, q[R].Ed = n, q[R].Sta = i;
    }
    printf("%lld\n", f[n]);
}

void Init() {
    scanf("%lld", &N);
    for(int i = 1; i <= N; i++) scanf("%d%d", &L[i].a, &L[i].b);
    sort(L + 1, L + N + 1, cmp);
    for(int i = N; i >= 1; i--)
    if(L[i].b > Land[n].b) {
        Land[++n].b = L[i].b;
        Land[n].a = L[i].a;
    }
}

int main() {
    Init();
    Dp();
    return 0;
}

Solution 2: 斜率优化

\[f(i) = \min_{j=0}^{i-1} \Big \{ f(j) + x[i]*y[j+1] \Big \}\]

令 $j < k$，决策 $k$ 比决策 $j$ 优的条件是：

\[f(k) + y[k+1] * x_i < f(j) + y[j+1] * x_i\] \[\Rightarrow \frac{f(k)–f(j)}{y[j+1] – y[k+1]} < x_i\]

令 $\text{Slope}(j,k)= \frac{f(k)–f(j)}{y[j+1]–y[k+1]} < x_i$，即当满足 $\text{Slope}(j,k) < x_i$ 时，决策 $k$ 就比决策 $j$ 优。

令 $j < k < L$，那么当 $\text{Slope}(j,k)>\text{Slope}(k,L)$ 时，决策 $k$ 可以舍去。也就是说只需要用队列维护决策 $p_1 < p_2 < p_3 < \dots < p_k$，使得 $\text{Slope}(p_1, p_2) < \text{Slope}(p_2, p_3)<…<\text{Slope}(p_{k-1}, p_k)$，即下凸包。

Code 2

Github (C++)

#include <iostream>
#include <cstdio>
#include <iomanip>
#include <cstring>
#include <algorithm>
#include <cmath>
using namespace std;

const int M = 50005;

struct node {
    long long a, b;
} L[M], Land[M];

long long f[M], q[M * 2];
int n, N;

bool cmp(node x, node y) {
    return x.a < y.a;
}

double Slope(int x, int y) {
    return (double(f[y] - f[x]) / double(Land[x + 1].b - Land[y + 1].b));
}

void Init() {
    scanf("%lld", &N);
    for(int i = 1; i <= N; i++) scanf("%d%d", &L[i].a, &L[i].b);
    sort(L + 1, L + N + 1, cmp);
    for(int i = 1; i <= N; i++) {
        while(n && Land[n].b <= L[i].b) n--;
        Land[++n] = L[i];
    }
}

void Dp() {
    int L = 1, R = 1, j;
    for(int i = 1; i <= n; i++) {
        while(L < R && Slope(q[L], q[L+1]) < Land[i].a) L++;
        j = q[L];
        f[i] = f[j] + (Land[j + 1].b) * (Land[i].a);
        while(L < R && Slope(q[R - 1], q[R]) > Slope(q[R], i)) R--;
        q[++R] = i;
    }
    printf("%lld\n", f[n]);
}

int main() {
    Init();
    Dp();
    return 0;
}

PREVIOUS竞赛